前言

学习资料：The Book of Shaders: Shaping functions

记录-color部分

vec4 vector;
vector[0] = vector.r = vector.x = vector.s;
vector[1] = vector.g = vector.y = vector.t;
vector[2] = vector.b = vector.z = vector.p;
vector[3] = vector.a = vector.w = vector.q;

支持swizzle(搅动)：vec3 yellow=vec3(1.,1.,0.); yellow.rgb, yellow.rgr, yellow.bgr ……

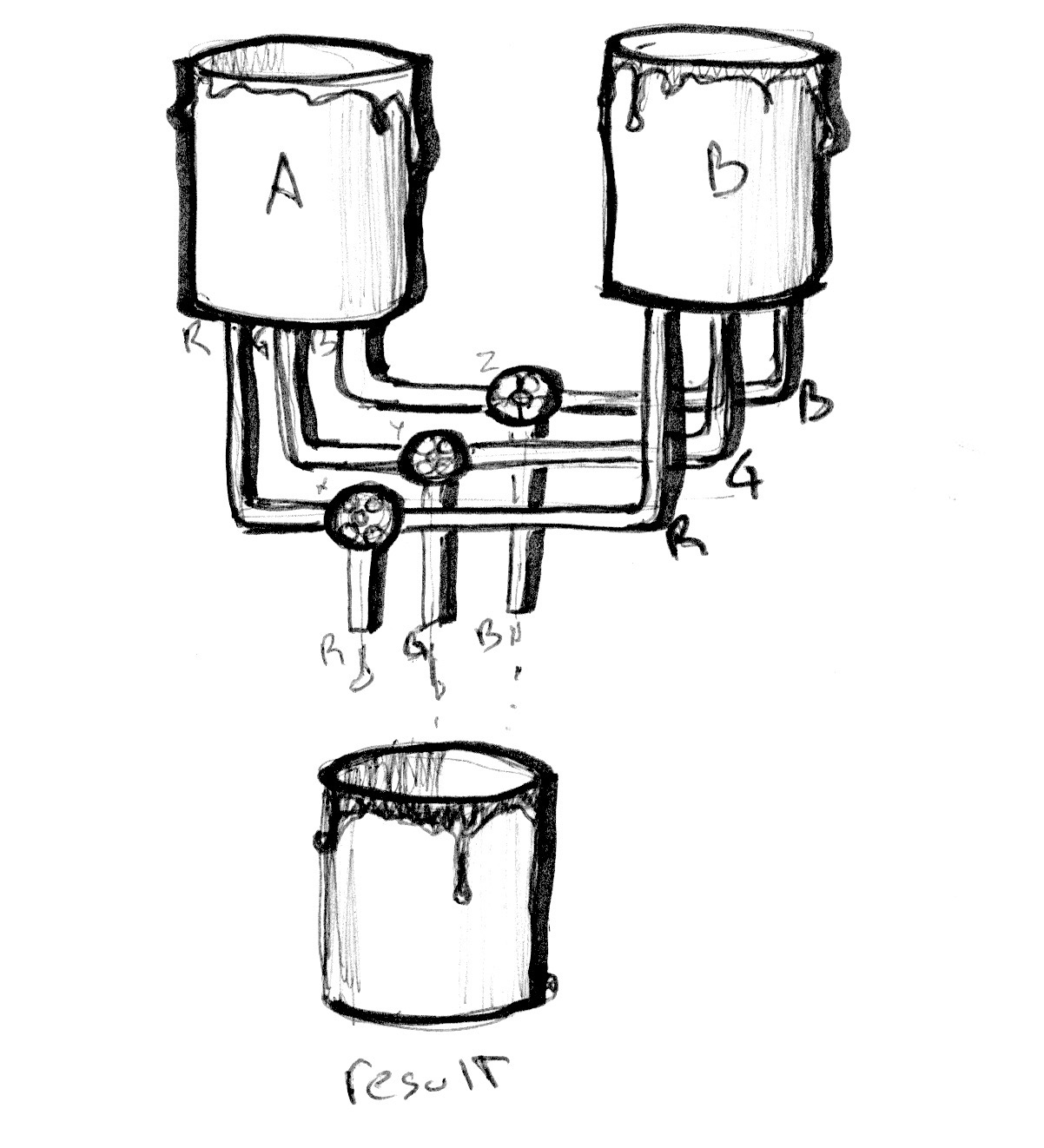
利用mix()进行color混合：mix(color1,color2,value) ，value从0到1，value越小color1值越多

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;
uniform float u_time;

vec3 colorA = vec3(0.149,0.141,0.912); // blue
vec3 colorB = vec3(1.000,0.833,0.224); // yellow

void main() {
    vec3 color = vec3(0.0);

    float pct = abs(sin(u_time)); // 从0到1，sin(x)

    // Mix uses pct (a value from 0-1) to
    // mix the two colors
    color = mix(colorA, colorB, pct);

    gl_FragColor = vec4(color,1.0);
}

easing function

用于计算动画的缓动函数easing function

下面的式子有些作者进行了sin/cos之间的变换，以及命名的风格是sineIn就是上面链接里的easeInSine
上面网页里，每个函数都有对应的css用法，postcss用法，在元素变换动画里的效果，在颜色渐变混合里的效果，使用该函数进行变换的样例（缩放、移动、透明度变化）,也可以调整参数点击go进行对比
最后一排：css的实现是通过@keyframes，设置不同的条件；函数里面是通过一系列的判断来赋值；
前四排的都是cube-bezier函数设置不同的参数得到的效果

在 CSS 中，cubic-bezier 函数用于定义一个三次贝塞尔曲线，广泛应用于动画和过渡效果的时间函数（timing function）。这个函数的四个参数控制曲线的形状，从而影响动画的速度变化。

具体来说，cubic-bezier(.12, 0, .33, 0) 中的四个参数表示的是两个控制点的坐标：

第一个控制点的坐标为 (0.12, 0)

第二个控制点的坐标为 (0.33, 0)

这四个参数可以这样解释：

**第一个参数 (0.12)**：这是第一个控制点的横坐标，它影响动画开始阶段的加速度。值为 0.12 表示在动画开始阶段，速度从零开始缓慢增加。

**第二个参数 (0)**：这是第一个控制点的纵坐标，它在这里设为 0，意味着控制点位于起始线上，因此动画起始时会比较平缓，没有立即加速。

**第三个参数 (0.33)**：这是第二个控制点的横坐标，影响动画结束前的减速过程。值较小（0.33）表明动画在结束前不久开始减速。

**第四个参数 (0)**：这是第二个控制点的纵坐标，同样为 0，意味着结束时速度减到 0，动画结束的过程也是比较平缓的。

通过调整这些参数，开发者可以精确控制动画的速度曲线，从而创造出各种动画效果。在这个具体例子中，由于两个控制点的纵坐标都是 0，这种曲线通常用于创建某些具有明显起始和结束阶段的动画效果。

#ifdef GL_ES
precision mediump float;
#endif

#define PI 3.141592653589793
#define HALF_PI 1.5707963267948966

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;

// Robert Penner's easing functions in GLSL
// https://github.com/stackgl/glsl-easings
float linear(float t) {
  return t;
}

float exponentialIn(float t) {
  return t == 0.0 ? t : pow(2.0, 10.0 * (t - 1.0));
}

float exponentialOut(float t) {
  return t == 1.0 ? t : 1.0 - pow(2.0, -10.0 * t);
}

float exponentialInOut(float t) {
  return t == 0.0 || t == 1.0
    ? t
    : t < 0.5
      ? +0.5 * pow(2.0, (20.0 * t) - 10.0)
      : -0.5 * pow(2.0, 10.0 - (t * 20.0)) + 1.0;
}

float sineIn(float t) {
  return sin((t - 1.0) * HALF_PI) + 1.0;
}

float sineOut(float t) {
  return sin(t * HALF_PI);
}

float sineInOut(float t) {
  return -0.5 * (cos(PI * t) - 1.0);
}

float qinticIn(float t) {
  return pow(t, 5.0);
}

float qinticOut(float t) {
  return 1.0 - (pow(t - 1.0, 5.0));
}

float qinticInOut(float t) {
  return t < 0.5
    ? +16.0 * pow(t, 5.0)
    : -0.5 * pow(2.0 * t - 2.0, 5.0) + 1.0;
}

float quarticIn(float t) {
  return pow(t, 4.0);
}

float quarticOut(float t) {
  return pow(t - 1.0, 3.0) * (1.0 - t) + 1.0;
}

float quarticInOut(float t) {
  return t < 0.5
    ? +8.0 * pow(t, 4.0)
    : -8.0 * pow(t - 1.0, 4.0) + 1.0;
}

float quadraticInOut(float t) {
  float p = 2.0 * t * t;
  return t < 0.5 ? p : -p + (4.0 * t) - 1.0;
}

float quadraticIn(float t) {
  return t * t;
}

float quadraticOut(float t) {
  return -t * (t - 2.0);
}

float cubicIn(float t) {
  return t * t * t;
}

float cubicOut(float t) {
  float f = t - 1.0;
  return f * f * f + 1.0;
}

float cubicInOut(float t) {
  return t < 0.5
    ? 4.0 * t * t * t
    : 0.5 * pow(2.0 * t - 2.0, 3.0) + 1.0;
}

float elasticIn(float t) {
  return sin(13.0 * t * HALF_PI) * pow(2.0, 10.0 * (t - 1.0));
}

float elasticOut(float t) {
  return sin(-13.0 * (t + 1.0) * HALF_PI) * pow(2.0, -10.0 * t) + 1.0;
}

float elasticInOut(float t) {
  return t < 0.5
    ? 0.5 * sin(+13.0 * HALF_PI * 2.0 * t) * pow(2.0, 10.0 * (2.0 * t - 1.0))
    : 0.5 * sin(-13.0 * HALF_PI * ((2.0 * t - 1.0) + 1.0)) * pow(2.0, -10.0 * (2.0 * t - 1.0)) + 1.0;
}

float circularIn(float t) {
  return 1.0 - sqrt(1.0 - t * t);
}

float circularOut(float t) {
  return sqrt((2.0 - t) * t);
}

float circularInOut(float t) {
  return t < 0.5
    ? 0.5 * (1.0 - sqrt(1.0 - 4.0 * t * t))
    : 0.5 * (sqrt((3.0 - 2.0 * t) * (2.0 * t - 1.0)) + 1.0);
}

float bounceOut(float t) {
  const float a = 4.0 / 11.0;
  const float b = 8.0 / 11.0;
  const float c = 9.0 / 10.0;

  const float ca = 4356.0 / 361.0;
  const float cb = 35442.0 / 1805.0;
  const float cc = 16061.0 / 1805.0;

  float t2 = t * t;

  return t < a
    ? 7.5625 * t2
    : t < b
      ? 9.075 * t2 - 9.9 * t + 3.4
      : t < c
        ? ca * t2 - cb * t + cc
        : 10.8 * t * t - 20.52 * t + 10.72;
}

float bounceIn(float t) {
  return 1.0 - bounceOut(1.0 - t);
}

float bounceInOut(float t) {
  return t < 0.5
    ? 0.5 * (1.0 - bounceOut(1.0 - t * 2.0))
    : 0.5 * bounceOut(t * 2.0 - 1.0) + 0.5;
}

float backIn(float t) {
  return pow(t, 3.0) - t * sin(t * PI);
}

float backOut(float t) {
  float f = 1.0 - t;
  return 1.0 - (pow(f, 3.0) - f * sin(f * PI));
}

float backInOut(float t) {
  float f = t < 0.5
    ? 2.0 * t
    : 1.0 - (2.0 * t - 1.0);

  float g = pow(f, 3.0) - f * sin(f * PI);

  return t < 0.5
    ? 0.5 * g
    : 0.5 * (1.0 - g) + 0.5;
}

void main() {
    vec3 colorA = vec3(0.149,0.141,0.912);
    vec3 colorB = vec3(1.000,0.833,0.224);

    float t = u_time*0.5;
    float pct = cubicInOut( abs(fract(t)*2.0-1.) );
 	  // t = u_time;
 	  // pct = cubicInOut( abs(fract(t)-1.) );
    gl_FragColor = vec4(vec3(mix(colorA, colorB, pct)),1.0);
}

补充说明：

float t = u_time * 0.5;
float pct = cubicInOut(abs(fract(t) * 2.0 - 1.0));

**时间缩放 (t = u_time * 0.5)**：这里 u_time 被乘以 0.5，意味着 t 的变化速度是 u_time 的一半。如果 u_time 是一个随时间增加的变量，那么 t 的增长速度更慢。
**计算 pct**：fract(t) 获取 t 的小数部分，这样即使 t 增长到 1 以上，fract(t) 也会重新从 0 开始，实现周期性重置。乘以 2.0 然后减 1.0 是为了将周期变化从 [0,1] 调整到 [-1,1]，这样 abs(...) 后的值将在 [0,1] 之间振荡，实现了先增加到 1 然后减少到 0 的周期性变化。
cubicInOut 动画曲线：这个函数通常定义了一个缓入缓出的三次曲线，意味着动画开始和结束时速度较慢，中间速度较快。

t = u_time;
pct = cubicInOut(abs(fract(t) - 1.0));

**时间设置 (t = u_time)**：这里没有对 u_time 进行缩放，因此 t 以原始速度增加。
**计算 pct**：这里仅使用了 fract(t) 减去 1.0，与上面的代码相比，这样处理会产生从 -1 到 0 的周期性变化（因为 fract(t) 产生 [0,1)，减 1 后变为 [-1,0)）。应用 abs(...) 后，变化将在 [0,1) 间发生，实现了周期性的从 0 增加到 1。

效果差异：

变化速率：上面的代码中 t 的变化速度为原始时间的一半，这导致整体动画速度更慢。
振荡方式：上面的代码使得振荡从 0 增加到 1 然后减少到 0，形成一个完整的循环，而下面的代码只从 0 增加到 1。

结合这些分析，上面的代码提供了一个更平滑和对称的振荡模式，适用于需要循环动画效果的场景，如呼吸灯效果。下面的代码则更适合于单向的渐进或渐出效果，如日出效果。

颜色的渐变

......
void main() {
    vec3 color = vec3(0.0);
	 vec2 st = gl_FragCoord.xy/u_resolution;
    float pct = cubicInOut(st.y); 
    pct = circularInOut(st.y); // 因为InOut那边的曲线是在很小范围内的自变量下发生了较大的因变量变化，所以分界线会明显，相对上面的来说
    // Mix uses pct (a value from 0-1) to
    // mix the two colors
    color = mix(colorA, colorB, pct);

    gl_FragColor = vec4(color,1.0);
}

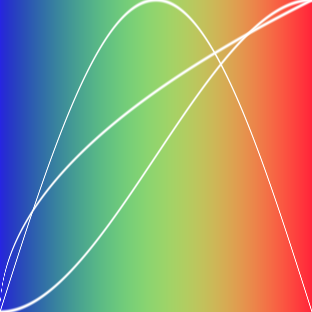
mix对RGB三个通道的控制

可以分别设置RGB三通道的混合方式

示例

#ifdef GL_ES
precision mediump float;
#endif

#define PI 3.14159265359

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;

vec3 colorA = vec3(0.149,0.141,0.912);
vec3 colorB = vec3(1.000,0.833,0.224);

float plot (vec2 st, float pct){
  return  smoothstep( pct-0.01, pct, st.y) -
          smoothstep( pct, pct+0.01, st.y); // smoothstep(a-极小值,a,纹理坐标)-smoothstep(a,a+极小值,纹理坐标)，可以画出a的曲线（也就是代码里的pct）
}

void main() {
    vec2 st = gl_FragCoord.xy/u_resolution.xy;
    vec3 color = vec3(0.0);

    vec3 pct = vec3(st.x);

    pct.r = smoothstep(0.0,1.0, st.x);
    pct.g = sin(st.x*PI);
    pct.b = pow(st.x,0.5);

    color = mix(colorA, colorB, pct);

    // Plot transition lines for each channel
    color = mix(color,vec3(1.0,1.0,1.0),plot(st,pct.r));
    color = mix(color,vec3(1.0,1.0,1.0),plot(st,pct.g));
    color = mix(color,vec3(1.0,1.0,1.0),plot(st,pct.b));

    gl_FragColor = vec4(color,1.0);
}

混合加变换的组合

......
void main() {
    vec3 color1 = vec3(0.149,0.141,0.912);
    vec3 color2 = vec3(1.000,0.833,0.224);
  
    vec2 st = gl_FragCoord.xy/u_resolution;
  
    vec3 colorA = mix(color1,color2,st.y);
    vec3 colorB = mix(color1,color2,1.-st.y*st.x);

    float t = u_time*0.5;
    float pct = cubicInOut( abs(fract(t)*2.0-1.) );
 	  // t = u_time;
 	  // pct = cubicInOut( abs(fract(t)-1.) );
    gl_FragColor = vec4(vec3(mix(colorA, colorB, pct)),1.0);
}

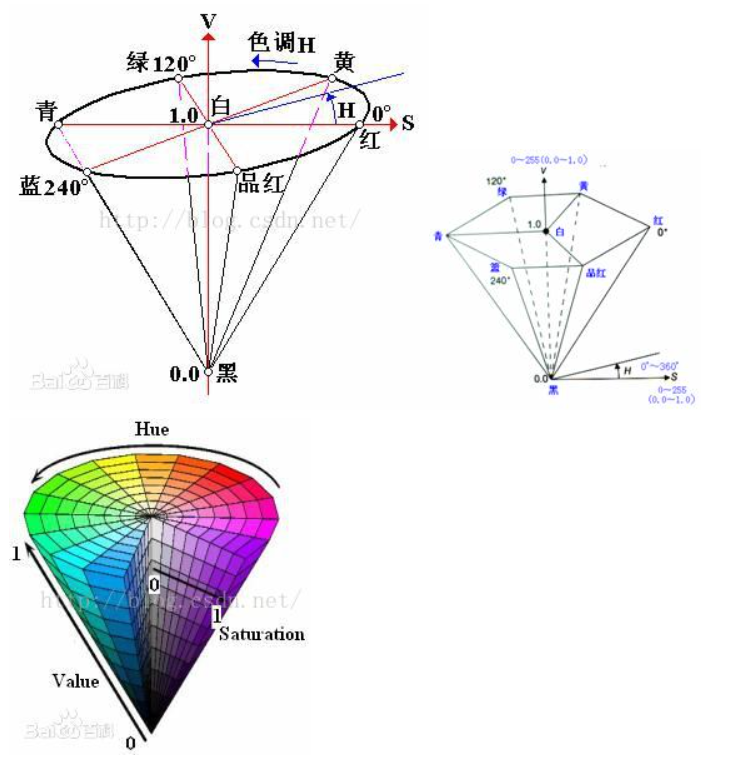
HSV

shadertoy代码：

Smooth HSV (shadertoy.com)

OpenCV学习笔记——HSV颜色空间超极详解&inRange函数用法及实战_hsv值是什么-CSDN博客

HSV色彩空间和颜色分量范围 - 友善的狗W - 博客园 (cnblogs.com)

RGB和HSV的互转

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;
uniform float u_time;

vec3 rgb2hsb( in vec3 c ){
    vec4 K = vec4(0.0, -1.0 / 3.0, 2.0 / 3.0, -1.0);
    vec4 p = mix(vec4(c.bg, K.wz),
                 vec4(c.gb, K.xy),
                 step(c.b, c.g));
    vec4 q = mix(vec4(p.xyw, c.r),
                 vec4(c.r, p.yzx),
                 step(p.x, c.r));
    float d = q.x - min(q.w, q.y);
    float e = 1.0e-10;
    return vec3(abs(q.z + (q.w - q.y) / (6.0 * d + e)),
                d / (q.x + e),
                q.x);
}

//  Function from Iñigo Quiles
//  https://www.shadertoy.com/view/MsS3Wc
vec3 hsb2rgb( in vec3 c ){
    vec3 rgb = clamp(abs(mod(c.x*6.0+vec3(0.0,4.0,2.0),
                             6.0)-3.0)-1.0,
                     0.0,
                     1.0 );
    rgb = rgb*rgb*(3.0-2.0*rgb);
    return c.z * mix(vec3(1.0), rgb, c.y);
}

void main(){
    vec2 st = gl_FragCoord.xy/u_resolution;
    vec3 color = vec3(0.0);

    // We map x (0.0 - 1.0) to the hue (0.0 - 1.0)
    // And the y (0.0 - 1.0) to the brightness
    color = hsb2rgb(vec3(st.x,1.0,st.y)); // 传入的体现了h,s,b

    gl_FragColor = vec4(color,1.0);
}

HSB从笛卡尔坐标映射到极坐标：

获取角度和到屏幕中心点的距离
使用length()和atan(y,x)

#ifdef GL_ES
precision mediump float;
#endif

#define TWO_PI 6.28318530718

uniform vec2 u_resolution;
uniform float u_time;

//  Function from Iñigo Quiles
//  https://www.shadertoy.com/view/MsS3Wc
vec3 hsb2rgb( in vec3 c ){
    vec3 rgb = clamp(abs(mod(c.x*6.0+vec3(0.0,4.0,2.0),
                             6.0)-3.0)-1.0,
                     0.0,
                     1.0 );
    rgb = rgb*rgb*(3.0-2.0*rgb);
    return c.z * mix( vec3(1.0), rgb, c.y);
}

void main(){
    vec2 st = gl_FragCoord.xy/u_resolution;
    vec3 color = vec3(0.0);

    // Use polar coordinates instead of cartesian
    vec2 toCenter = vec2(0.5)-st; // 把纹理坐标空间移到-.5到.5
    float angle = atan(toCenter.y,toCenter.x); // 求每个点相对于中心点的角度
    float radius = length(toCenter)*2.0; // 长度的范围是0~1

    // Map the angle (-PI to PI) to the Hue (from 0 to 1)
    // and the Saturation to the radius
    color = hsb2rgb(vec3((angle/TWO_PI)+0.5,radius,1.0)); // 第一个表示h，根据相对于中心点的角度来赋予颜色，同时缩放到了0-1，然后传入；radius: 离中心点越远，radius越大，s值越大;

    gl_FragColor = vec4(color,1.0);
}