初探即退之图形学Ⅰ|Games101
通过Games101接触的图形学,前面还是认真上的,后面,特别是到路径追踪之后,就粗糙过了一遍。总体感受还是劝退,就当对图形学有了一个基本的感受吧,有些特别是偏物理的,本人的确不行,即使从头来,时间成本有点大。
看后续需要吧,在本人找工作的大背景下,以及对个人优势的追求下,这部分现阶段显得无足轻重。
点击课程链接,跳转Games101课程;在线平台指路;课程复习跟看。
Overview
助教简介:信息网站website、研究领域research
怎么判断画面好?
看画面亮不亮,如果亮,说明全局光照设置的好,整个看起来就亮
special effects 特效
字体 Typography, the quick brown fox jumps over the lazy dog. 这句话里面包括了 26 个字母,所以会经常用于字母的字体测试。
CG:是什么?有什么用?应用在哪些地方?
Course
- Rasterization, OpenGL, shader
光栅化,用于将三维地理实体 geometry primitives投影到屏幕上,并转换为像素 fragments/pixels,在实时应用中很常见 real-time applications
主要是投影
- Curves and Meshes
如何表达曲线、曲面,来构造几何
- Ray Tracing
光线追踪,计算相交和阴影,在动画和电影中很多应用,可以达到好的效果,但比较慢,是一种 trade off, 用于 offline applications
如何实现时间和效果的双赢,现在有实时光线追踪
- Animation/Simulation
关键帧动画,弹珠弹跳,物体悬挂模拟
We learn graphics, not graphics apis(OpenGL, DirectX, Vulcan)
3D modeling: Maya, 3dMax, Blender
VR/game development: Unity/UE
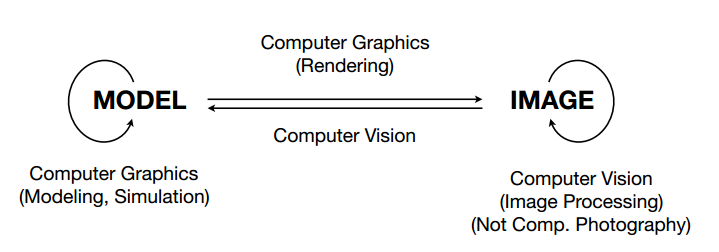
CG & CV(有区别,但没有明确边界):
一切需要猜测的内容,都属于计算机视觉里面的在做的
图像层面的工作也不在图形学里面
极客: geek, genius 天才, freak 怪胎
Linear algebra review
A swift and brutal introduction to linear algebra 线性代数简单入门
图形学依赖于:
基础数学,线性代数,统计
基础物理,光学和力学
一点美学
向量,矢量 vector
向量表示,向量构成,向量加减,向量坐标表示, 默认向量是列向量。
vector dot product点乘
在 unity vector 里,两个单位向量乘积就是夹角余弦;向量属性
作用:求夹角、求投影(可以算两个向量多么接近,可以分解一个向量,可以判断向量的方向前还是后 determine forward or backward
cross product 叉乘
Right-hand rule,右手法则, unity 是左手法则
不满足交换律,分配和结合律存在
作用: determine left/right, determine inside/outside(根据多个左右判断来确定内外),是三角形光栅化的基础
corner case,就是刚好在边上,这个自己说了算
点乘和叉乘
可以用来定义坐标系, orthonormal coordinate frames,并求向量
矩阵 matrices
m*n, m rows and n columns
Matrix-matrix multiplication: the dot product of row i from A and column j from B,A 矩阵的行和 B 矩阵的列的点乘
矩阵乘积无交换律
矩阵转置
单位矩阵,identity matrix
矩阵的逆
用来进行变换:translation, rotation, shear, scale
向量的运算转换为矩阵的形式
transformation
why transformation
Modeling: Translation, Rotation, Scaling
Viewing: (3D to 2D) projection
2D transformation
Scale matrix(include non-uniform) 缩放
Reflection matrix 反射/对称
shear matrix 切变,有弹性
rotate(原点,逆时针)
如果一个矩阵的逆等于它的转置,那这个矩阵被叫为正交矩阵;
齐次坐标 Homogeneous coordinates
translation, not linear transform,平移不是线性变换,不能用上面的那种方式表示
为了把这些都放在一起表示,所以使用了齐次坐标;
对二维的增加一个维度,用这个维度来表示 translation;
如何增加这个第三维,是 0 还是 1
2D point: (x,y,1)
2D vector: (x,y,0)
所有的仿射变换 affine map,都可以写成齐次坐标的形式
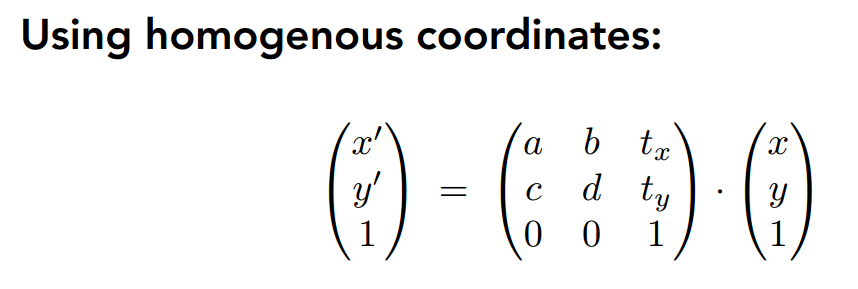
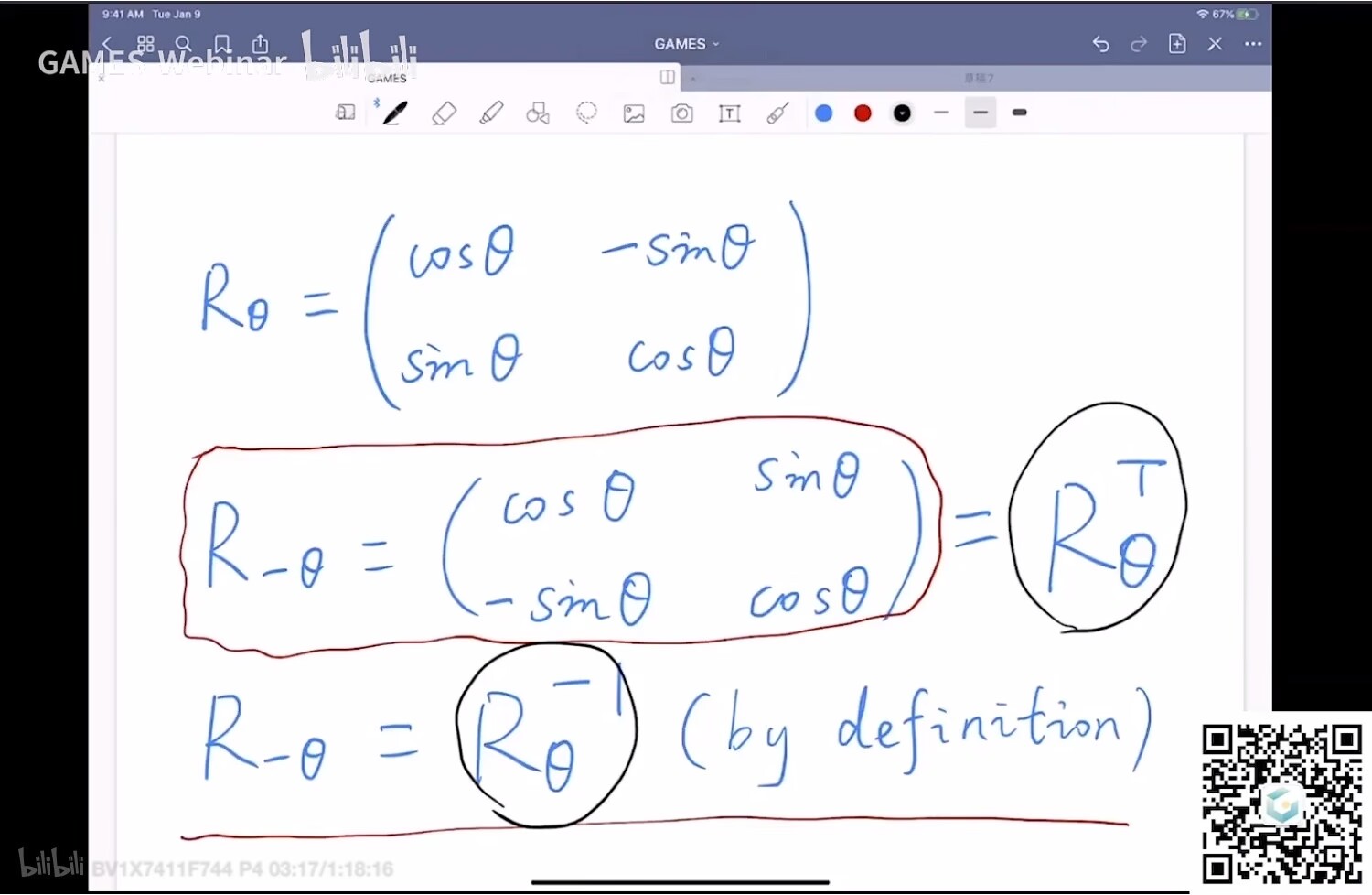
逆变换
composing transform 变换的组合
左乘进行变换,先旋转后平移
把左乘的所有矩阵进行组合,形成一个 3*3 的矩阵,来代表变换的组合
绕着给定点旋转,可以移动到原点,旋转,再移回给定点
3D transform
和二维同理,添加第四维的坐标 0 或者 1
三维普通旋转:把任意的旋转分解到 xyz 三个方向, rodrigues’ rotation formula。可以把绕着旋转的点移到原点,再移回去。
viewing transform 视图变换+投影变换
MVP 变换
Think about how to take a photo:
- Find a good place and arrange people (model transformation)
- Find a good “angle” to put the camera (view transformation)
- Cheese! (projection transformation)
view/camera transformation
把相机固定在原点,向着- Z 看,向上方向是 Y;
设置物体的移动,利用了相对论;
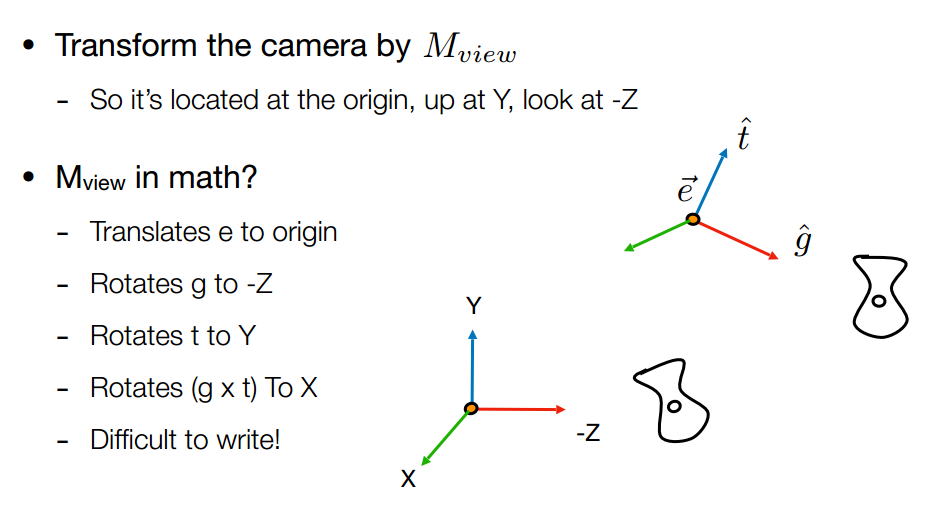
原始的变换不好求,求变换;
视图变换的表达view transformation:

其他物体也进行相同的变换model transformation;
这样就能实现相机固定,相机和物体保持相对状态;
projection transformation
为什么需要进行model/view变换
from 3D to 2D
orthographic projection 正交投影
左手系,所以 near is larger than far(in a value),在数值上近处的比远处的大
方式 1: 扔掉 Z 轴,但需要区分前后;之后固定到-1,1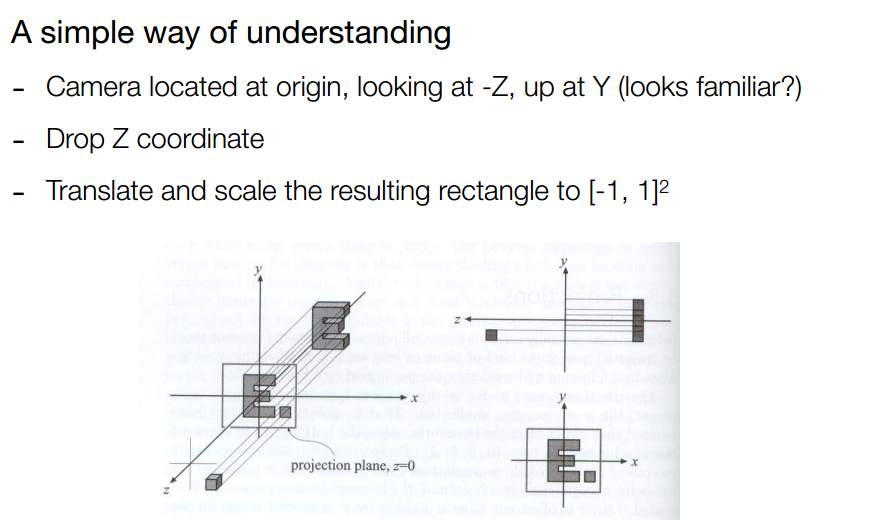
方式 2: 构造 canonical cube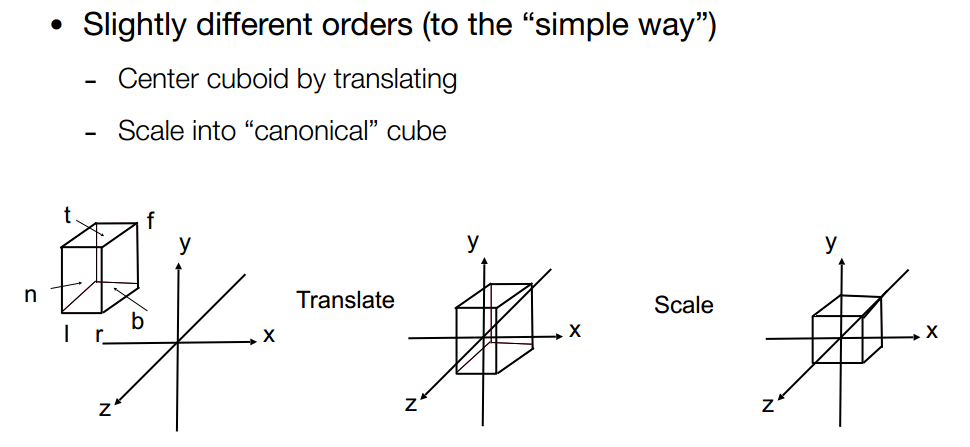
移动中点,设置缩放范围为 2
perspective projection 透视投影
近大远小
投影过程:先挤之后正交投影
挤的规定:近平面不变,远平面的 Z、中心点不变
aspect ratio = width/height
Field of view 视角,垂直视角 vertical field of view, fovY
通过定义这两个变量,就可以表示出其他的变量







